Hubungan Antara Rusuk Kubus Dengan Luas Permukaan Kubus Adalah

Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang berbentuk persegi. Ciri-ciri kubus adalah memiliki enam sisi yang sama dan setiap sudutnya berukuran 90 derajat. Salah satu konsep penting dalam geometri kubus adalah hubungan antara panjang rusuknya dengan luas permukaannya. Konsep ini memainkan peran penting dalam berbagai aplikasi, seperti menghitung volume dan luas permukaan kubus.

Rumus Hubungan Rusuk dan Luas Permukaan Kubus

Hubungan antara panjang rusuk kubus (s) dengan luas permukaannya (L) dapat dinyatakan dengan rumus berikut:

```
```

Penjelasan Rumus

Rumus tersebut menunjukkan bahwa luas permukaan kubus berbanding lurus dengan kuadrat panjang rusuknya. Artinya, jika kita menggandakan panjang rusuk kubus, luas permukaannya akan meningkat empat kali lipat. Sebaliknya, jika kita mengurangi setengah panjang rusuknya, luas permukaannya akan berkurang menjadi seperempat.

Contoh Penerapan Rumus

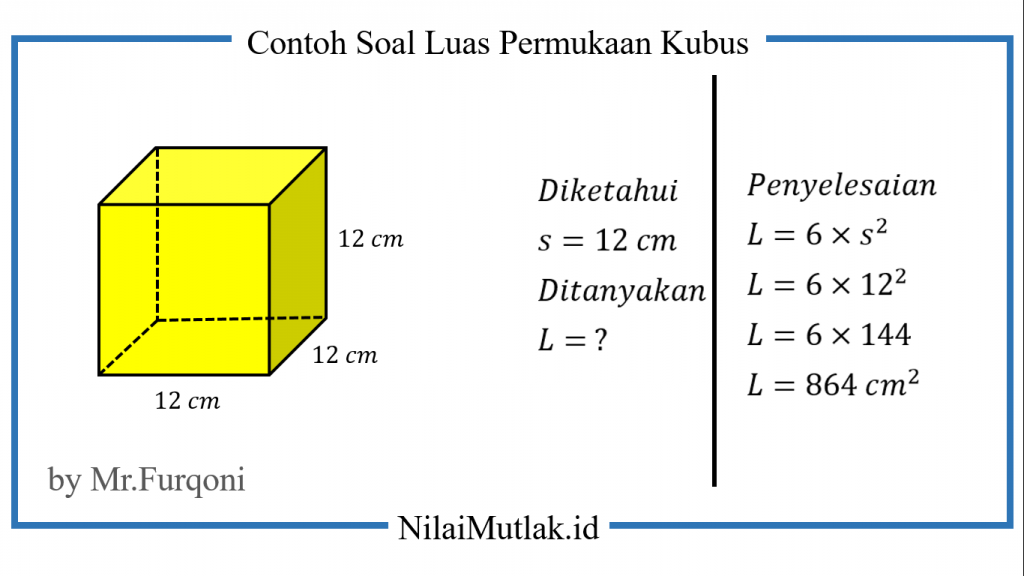
Misalkan kita memiliki kubus dengan panjang rusuk 5 cm. Berapakah luas permukaan kubus tersebut?

```
= 150 cm^2
```

Jadi, luas permukaan kubus dengan panjang rusuk 5 cm adalah 150 cm².

Faktor yang Mempengaruhi Luas Permukaan Kubus

Selain panjang rusuk, faktor lain yang dapat memengaruhi luas permukaan kubus adalah sebagai berikut:

1. Jumlah Sisi

Kubus memiliki enam sisi persegi, sehingga luas permukaannya selalu lebih besar daripada bangun ruang lain dengan jumlah sisi yang sama.

2. Ukuran Sisi

Semakin besar ukuran sisi persegi yang membentuk kubus, semakin besar pula luas permukaannya.

3. Bentuk Persegi

Karena kubus dibatasi oleh enam persegi yang sama, bentuknya tetap dan tidak dapat diubah. Hal ini menentukan luas permukaan kubusnya.

Pentingnya Memahami Hubungan Antara Rusuk dan Luas Permukaan Kubus

Memahami hubungan antara panjang rusuk dan luas permukaan kubus sangat penting karena memungkinkan kita untuk:

Kesimpulan

Sampai jumpa kembali di artikel menarik lainnya!

FAQ

Hubungan tersebut menyatakan bahwa luas permukaan kubus berbanding lurus dengan kuadrat panjang rusuknya.

Jumlah sisi, ukuran sisi, dan bentuk persegi.

Untuk menghitung luas permukaan, volume, dan menganalisis sifat-sifat geometri kubus.

Dalam arsitektur, desain produk, dan perhitungan teknis.